3. Paramètres statistiques d'une distribution
Lorsque l’on est en face d’une série statistique comportant un grand nombre de termes, il devient difficile d’analyser directement l’ensemble des données. Nous avons vu que la représentation graphique permettait d’extraire une certaine information. En complément de cette analyse qualitative, le statisticien est amené à simplifier la distribution observée par des caractéristiques significatives. Nous distinguerons deux types de caractéristiques : celles de la tendance centrale et celles de dispersion.
3.1. Caractéristiques de la tendance centrale
La plus importante est la moyenne arithmétique. Elle se calcule en additionnant les différentes valeurs de la série statistique et en divisant ce nombre par l’effectif total de la série. L’expression mathématique de la moyenne s’écrit de la façon suivante :
Le symbole mathématique ∑ est l’opérateur somme et indique que l’on doit additionner toutes les valeurs prises par la variable X.Prenons l’exemple d’une série de dosages ayant donné pour résultat :
10, 15, 11, 16, 9, 8, 14, 7, 13
Cette série comportant 9 valeurs, sa moyenne est calculée de la façon suivante :
soit
Dans le cas d’une série statistique où plusieurs valeurs se répètent dans la série, on utilise une formule plus adaptée correspondant à la moyenne arithmétique pondérée.
Si l’on obtient la série de dosage suivante :
10, 6, 15, 15, 8, 9, 10, 12, 15, 18, 14, 14, 13
on peut regrouper les valeurs identiques et former le tableau suivant :
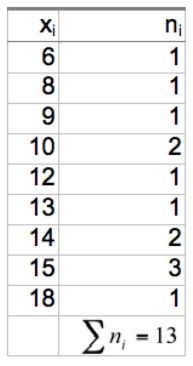
La formule pour le calcul de la moyenne devient
; cette formule indique que l’on va pondérer chaque valeur prise par la variable X par sa fréquence absolue .
![]()
Le calcul est identique lorsque les données sont réparties en classes. Dans l’exemple de la distribution des poids de naissance des nouveau-nés, on peut dresser le tableau suivant :
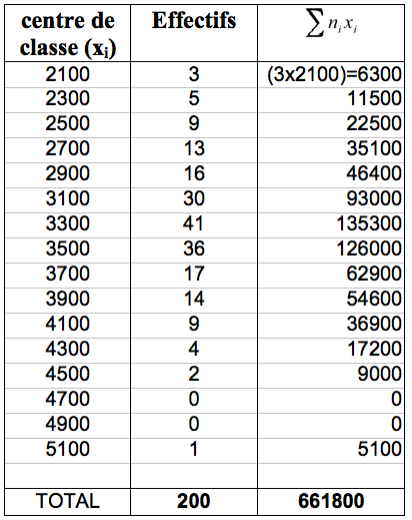
La moyenne se calcule ainsi :
On remarquera que lorsque les données sont réparties en classe, le terme ni/n représente la fréquence relative d’une valeur xi de la distribution.
Dans le cas des variables discontinues, le calcul de la moyenne est identique au cas précédent portant sur des variables continues.
Elle sont liées aux propriétés de l’opérateur somme. Ainsi on peut montrer que :
a) si chaque valeur de la variable X est affectée d’un coefficient constant a :
; cela donne pour la moyenne :
b) Si l’on retranche une constante a à chaque valeur de la variable X
soit pour la moyenne
Ces deux propriétés vont être utilisées pour simplifier le calcul de la moyenne dans le cas de séries statistiques comportant un grand nombre de termes.
c) La somme algébrique des écarts d'un ensemble de valeurs à leur moyenne arithmétique est nulle : ainsi pour la série 14, 10, 8, 7, 11 où la moyenne est 10, on s'aperçoit qu'en calculant la somme des écart de chacune des valeurs par rapport à la moyenne, on obtient une valeur nulle.
d) La somme des carrés des écarts d'un ensemble de valeurs à leur moyenne arithmétique est minimale.
= valeur minimale
e) La moyenne d’une population P constituée de plusieurs sous-populations P1, P2... de moyennes peut s’exprimer en fonction des moyennes ... de chacune des sous-populations
Deux autres caractéristiques de la tendance centrale peuvent être définies : ce sont le mode et la médiane.
Le mode correspond à la valeur particulière de la variable aléatoire pour laquelle la fréquence est maximale dans la distribution observée.
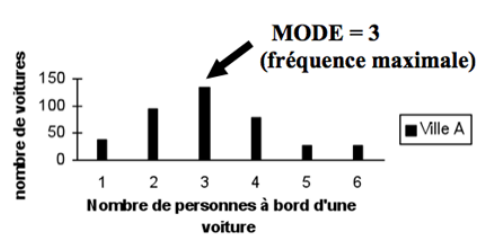
La médiane est la valeur de la variable aléatoire telle que, dans une distribution donnée, il y ait autant de valeurs supérieures et inférieures à cette médiane.
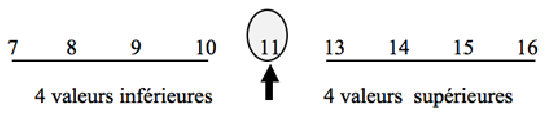
Dans le cas où la série comporte un nombre pair de données, on calcule la médiane en divisant par 2 la somme des 2 valeurs centrales de la série.
3.2. Caractéristiques de la dispersion
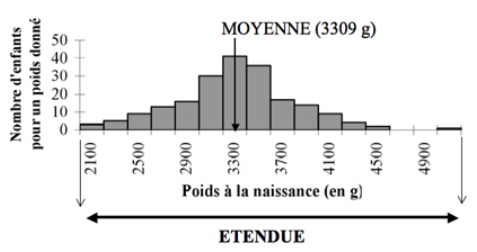
Dans cet exemple, où nous avons déjà calculé la moyenne (représentée par une flèche sur l’axe des abscisses), on constate une dispersion des valeurs autour de cette tendance centrale.
Cette dispersion peut être quantifiée de façon grossière par l'étendue de la distribution, c'est à dire par la différence entre les deux valeurs extrêmes de la distribution. Ici l'étendue serait 5200-2000=3200 g. Cet indicateur n'est cependant pas suffisamment précis pour caractériser la dispersion surtout lorsque le nombre d'observations devient important.
On est donc amené à trouver une autre caractéristique pour exprimer la variabilité du caractère quantitatif étudié. On peut s’intéresser par exemple à l’ensemble des écarts e par rapport à la moyenne (e=x-μ ). On a montré précédemment que la moyenne de ces écarts était nulle ; on pourrait alors utiliser la moyenne de la valeur absolue des écarts (qui serait toujours positive). Cet indicateur n’est cependant pas d’un maniement aisé car il se prête mal aux calculs algébriques. On préfère donc un autre indicateur qui met en jeu la somme des carrés des écarts que l’on va rapporter au nombre n d’écarts dans la distribution.
Cette caractéristique est appelée variance et se note σ2 . On la calcule comme suit :
Plus les valeurs sont dispersées autour de la moyenne, plus les écarts autour de la moyenne sont importants. En élevant ces écarts au carré, on amplifie encore l’importance des écarts, ce qui donne plus de poids aux valeurs éloignées de la moyenne.
Le fait d'avoir élevé au carré les écarts à la moyenne donne à la variance des unités qui ne sont plus en accord avec celles de la distribution de départ (gramme2 pour la variance du poids des nouveau-nés). Pour remédier à ce problème, il est courant d'exprimer l'écart type qui est la racine carrée de la variance et dont les unités sont homogènes avec celles de la distribution.
a) cas ou les valeurs prises par la variable ne sont pas répétées.
Reprenons la série statistique donnée précédemment :
MOYENNE
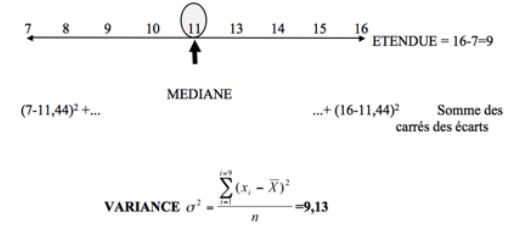
Dans le calcul effectué, on peut remarquer que la moyenne est arrondie avec deux chiffres significatifs. Si l’on avait utilisé tous les chiffres significatifs, le calcul aurait donné un résultat égal à 10,27. Cela vient du fait qu’en arrondissant la moyenne, on glisse une erreur qui est élevée au carré dans le calcul. Cette erreur dépend également du nombre de chiffres significatifs (choix arbitraire) que l’on donne à la moyenne.
Il est donc préférable pour calculer la variance d’utiliser un autre mode de calcul qui ne nécessite pas la valeur numérique de la moyenne. On peut utiliser la formule suivante obtenue après développement (voir complément) de la somme du carré des écarts.
Il est relativement facile d’utiliser cette formule de la variance lorsque l’on a pris soin de classer les données statistiques dans un tableau ayant la présentation suivante :

On montre que les n termes du numérateur de la variance peuvent être transformés par les relations suivantes :
...
En remplaçant dans le deuxième membre, par sa valeur , on obtient :
b) cas des données réparties en classes avec répétition de valeurs
Dans ce cas on est amené à pondérer chaque valeur prise par la variable X par sa fréquence absolue. La variance est donnée par la formule
Les calculs restent les mêmes que précédemment mais nécessitent une démarche rigoureuse. Dans l’exemple concernant l’occupation des véhicules dans une ville A on met en place le tableau suivant.

Il ne reste plus ensuite qu’à appliquer la formule de la variance.
(La moyenne pouvait également se calculer directement à partir du tableau )
3.3. Coefficient de variation
La valeur de l’écart type est bien sûr liée à la grandeur de la variable X. Elle est d’autant plus petite que la valeur mesurée est faible. Mais cela ne permet pas de comparer la dispersion de deux séries dont l’une présente des valeurs élevées et l’autre des valeurs petites. Pour obtenir un renseignement sur la dispersion relative des données on peut calculer le coefficient de variation qui exprime l’écart type par rapport à la moyenne des résultats. Il est généralement exprimé en pourcentage.La formule utilisée est la suivante :
3.4. calcul des paramètres statistiques après changement de variable
Le calcul de la moyenne ou de la variance peut vite devenir fastidieux lorsque les nombres manipulés ont des valeurs élevées. On est souvent amené à simplifier les données pour éviter les erreurs de calcul. Pour cela, un moyen simple est d’effectuer un changement de variable. Classiquement ce changement de variable fait intervenir le mode (x0) de la distribution (si les données se répètent ou sont réparties en classe) et l’amplitude de classe (h) (variable quantitative répartie en classe)Dans la distribution des poids de naissances on obtient le tableau suivant :
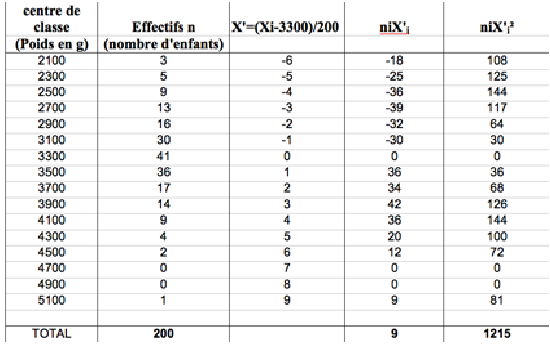
On calcule alors une moyenne provisoire :
La moyenne définitive est retrouvée en utilisant les propriétés arithmétiques de la fonction somme :
De même pour la variance :
Vérification des calculs :
Une erreur de calcul importante sur la moyenne est relativement facile à déceler car l’observation des données permet de donner un ordre de grandeur à ce paramètre. Ce n’est pas aussi évident pour la variance. Un des moyens de vérifier l’ordre de grandeur de la variance est d’utiliser une méthode basée sur l’analyse de l’étendue de la distribution. Dans l’exemple précédent, nous avions trouvé comme étendue une valeur de 3200 g. La table donnant la relation entre l’étendue et l’écart type (voir en annexe) donne un facteur de multiplication de l’étendue qui permet d’estimer la valeur de l’écart type (et donc de la variance). La distribution étudiée comportant 200 individus, on multiplie le nombre 3200 par 0,182 (donné dans la table) et l’on obtient 582,4 (ce qui est différent mais pas trop éloigné de la valeur exacte (494). Ce calcul suppose cependant une condition que l’on définira par la suite : la normalité de la distribution
3.5. Estimation des paramètres statistiques
Nous avons décrit jusqu’à maintenant le mode de calcul général permettant d’obtenir les paramètres d’une série statistique sans s’attacher à l’origine de cette série (population ou échantillon).
On exprimera respectivement par les symboles μ et σ2 la moyenne et la variance de la POPULATION.
Dans le cas où la série statistique correspond aux valeurs mesurées dans un échantillon extrait d'une population, on ne dispose alors que d'une partie plus ou moins importante des données qui dépend de la taille de l'échantillon et de celle de la population (qui est souvent très grande et inconnue). Il existe alors une incertitude sur les valeurs des paramètres statistiques calculés sur la base des données de l'échantillon. Il est en effet très peu probable que la moyenne et la variance dans l'échantillon soient exactement identiques à celles de la population mère. On peut donc au mieux ESTIMER les paramètres statistiques de cette population mère et essayer d'obtenir une valeur approchée de ces paramètres.
Pour la moyenne on considère que la valeur calculée dans l'échantillon (que l'on pourra appeler m ou ) est une bonne estimation de la moyenne de la population.
En revanche le calcul de la variance tel qu'il a été décrit précédemment, fait intervenir la somme des carrés des écarts à la moyenne qui est minimale (propriété de la moyenne arithmétique). Cette somme est donc par définition inférieure à la somme des écarts qui aurait été calculée avec la vraie valeur μ de la population (valeur proche mais différente de m). L’estimation de σ2 par le quotient est donc trop faible par rapport à la vraie valeur de la population (on dit que cette estimation introduit un biais ou que le paramètre est biaisé). On démontre que la meilleure correction consiste à jouer sur le dénominateur de la formule en diminuant d’une unité la taille n de l’échantillon.
Dans ces conditions, la variance estimée de la population (appelée s2) se calcule de la façon suivante : ,pour une variable dont les valeurs ne sont pas répétées ou ne sont pas réparties en classes, ou par la relation : , si les données se répètent ou sont classées.
On se rend compte facilement que lorsque l’échantillon est de taille importante (pratiquement n>30) il devient indifférent de prendre n ou (n-1) comme dénominateur de la variance.Il est en revanche important d’être rigoureux sur la notation lorsque que l’on estime les paramètres d’une population.
